集合と写像#
関係データベースのデータモデルである関係データモデルは,代数学,特に集合と写像に関する数学理論に支えられている. 関係データモデルを理解するためにはこれらの知識が必要となるため,以下,最低限必要となる集合と写像の知識を説明する.
以下の説明はかなり形式的である. 当たり前のことを記号をふんだんに使って説明しているが,物事を抽象化して捉えるためには記号的(数学的)な道具が必要になるので,嫌がらず読んでほしい(ただし気負いすぎないこと). なお,集合と写像について知識がある読者は,本節を読み飛ばしても問題ない.
集合#
数学における集合(set) とは,何かを集めたものである. 集合を構成する個々の「何か」は 要素(あるいは元; element) と呼ばれる.
例えば,以下は集合の例である.
\(\{1, 2, 3\}\)
上記集合は整数1,2,3を要素として集めたものである. 1,2,3はそれぞれ集合{1, 2, 3}の要素である. 一般に,集合は波カッコの中に要素を並べて表現する.
集合には名前がつけられる. 例えば,上記集合について
\(A = \{1, 2, 3\}\)
とすれば,集合\(\{1, 2, 3\}\)を集合Aと呼ぶことができる. なお,慣習上,集合をアルファベットで表すときは大文字アルファベット1文字,集合の要素をアルファベットで表すときは小文字アルファベット1文字を使う(例外ケースもある).
ある要素がある集合に属していることは,記号\(\in\)を用いて表現する. 例えば,整数1が集合Aに属していること(つまり集合Aの要素であること)は
\(1 \in A\)
と書ける. 一方,ある要素がある集合に属して「いない」ことは,記号\(\notin\)を用いて表現する. 例えば,整数7が集合Aに属していないことは
\(7 \notin A\)
と書ける.
集合の要素は数に限らない. 例えば,以下の平仮名集合Hのように文字の集合もありうる.
\(H = \{あ, い, う, え, お, ...., わ, を, ん\}\)
なお,集合の要素間の順序関係は無視される[1]. それゆえ,集合\(A=\{1, 2, 3, 4, 5\}\)と\(B=\{5, 4, 3, 2, 1\}\)はまったく同じ集合となる. つまり,
\(A=B\)
となる. また,(数学的な定義の)集合の要素は重複してはならない[2]. 重複する要素があった場合は,重複は無視して扱われる. 例えば,\(A=\{1, 3, 5, 7, 7\}\)は\(A=\{1, 3, 5, 7\}\)として扱われることになる.
集合の外延的定義と内包的定義#
集合の定義(表記)方法には2種類ある.
1つは外延的定義である. これは,集合の要素を具体的に列挙することで集合を定義する方法である. 例えば,
\(A = \{2, 4, 6, 8, 10, 12, 14, 16, 18, 20\}\)
は「20以下の偶数」である集合Aを外延的定義によって定義したものである. 外延的定義では集合の要素をすべて列挙するのが大変なため,以下のように途中の要素をテンテンで省略して書く場合もある.
\(A = \{2, 4, 6, ..., 18, 20\}\)
2つめの定義方法は内包的定義である. 外延的定義では要素を具体的に列挙するのに対して,内包的定義では集合の要素が満たすべき条件(性質)を示すことで集合を定義する. 例えば,前述の集合Aであれば,
\(A = \{ 2n \ | \ nは整数かつ0\leq n \leq 10\}\)
と書ける.内包的定義では波カッコの中を縦棒(|)で区切り,左側に集合の要素を表す文字を書き,右側には要素に関する条件を書く. なお,条件のAND(「かつ」)は以下のようにカンマで書くこともある.
\(A = \{ 2n \ | \ nは整数, 0\leq n \leq 10\}\)
よく使われる数の集合#
整数,自然数のように,よく使われる数の集合には特別な集合名が付けられている. 以下,代表的な数の集合を列挙しておく.
\(\mathbb{Z}\)は,整数全体をあらわす集合である. すなわち,
\(\mathbb{Z} = \{..., -2, -1, 0, 1, 2, ... \}\).
例えば,\(-7 \in \mathbb{Z}\)であり,\(0.3 \notin \mathbb{Z}\)である.
\(\mathbb{N}\)は,自然数全体をあらわす集合である. すなわち,
\(\mathbb{N}= \{1, 2, 3, ... \} = \{ n \ | \ n \in \mathbb{Z}, n \geq 1 \}\).
\(\mathbb{R}\)は,実数全体をあらわす集合である. 例えば,\(\sqrt{3} \in \mathbb{R}\),\(\pi \in \mathbb{R}\),\(e \in \mathbb{R}\)であり,\(1+1i \notin \mathbb{R}\),\(文字 \notin \mathbb{R}\)である(★Quiz1★,★Quiz2★).
空集合#
要素を持たない集合も集合である. そのような集合を空集合と呼ぶ. 空集合は\(\phi\)で表す. すなわち,
\(\phi = \{\}\).
集合の要素数#
集合Xの要素数は,\(|X|\)と表記する. 例えば\(A=\{1, 2, 3, 4, 5\}\)のとき,\(|A|=5\)である. また,
\(Z_n = \{0, 1, 2, 3, ...., n-1\} = \{x \ | \ x \in \mathbb{Z}, 0 \leq x \le n \}\)
のとき,\(|Z_n| = n\) となる.
要素を持たない集合も集合である. そのような集合を空集合と呼ぶ. 空集合は\(\phi\)で表す. すなわち,
\(\phi = \{\}\).
積集合(集合の共通部分)#
2つの集合A,Bが与えられたとき,集合A,Bに共通の要素を集めた集合を積集合(あるいは共通集合; intersection) と呼ぶ. 集合Aと集合Bの積集合は\(A \cap B\)と記す. 積集合\(A \cap B\)の内包的定義は以下の通り:
\(A \cap B = \{ x \ | \ x \in A かつ x \in B\}\)
以下の図は,集合\(A=\{2, 4, 6, 8, 10\}\)と集合\(B=\{4, 8, 12, 16, 20\}\)の積集合\(A \cap B\)をベン図で表している. このケースでは\(A \cap B = \{4, 8\}\)となる.
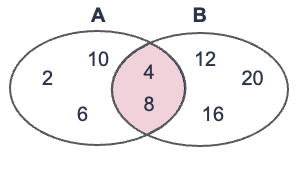
和集合#
2つの集合A,Bが与えられたとき,集合A,Bのいずれかに属する要素を集めた集合を和集合(union) と呼ぶ. 集合Aと集合Bの和集合は\(A \cup B\)と記す. 和集合\(A \cup B\)の内包的定義は以下の通り:
\(A \cup B = \{ x \ | \ x \in A または x \in B\}\)
以下の図は,集合\(A=\{2, 4, 6, 8, 10\}\)と集合\(B=\{4, 8, 12, 16, 20\}\)の和集合\(A \cup B\)をベン図で表している. このケースでは\(A \cup B = \{2, 4, 6, 8, 10, 12, 16, 20\}\)となる.
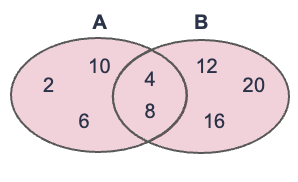
差集合#
2つの集合A,Bが与えられたとき,集合Aには属しているが集合Bには属していない要素を集めた集合をBからAを引いた差集合(set difference) と呼ぶ. 集合Bから集合Aを引いた差集合を\(B-A\)または\(B \setminus A\)と記す. 差集合\(B-A\)の内包的定義は以下の通り:
\(B-A = \{ x \ | \ x \in B かつ x \notin A\}\)
以下の図は,集合\(A=\{2, 4, 6, 8, 10\}\)から集合\(B=\{4, 8, 12, 16, 20\}\)を引いた差集合\(A-B\)をベン図で表している. このケースでは\(A-B = \{2, 6, 10\}\)となる.
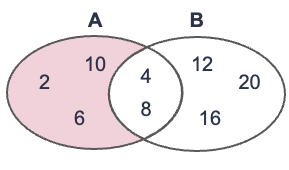
以下は,集合Bから集合Aを引いた差集合\(B-A\)を表したベン図である. このケースでは\(B-A = \{12, 16, 20\}\)となる. 2つの図を比較したら分かるように,差集合\(A-B\)と\(B-A\)は異なる(★Quiz3★).
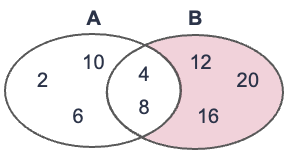
部分集合#
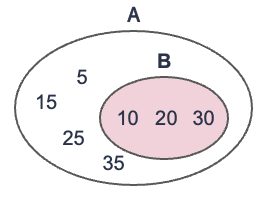
2つの集合A,Bが与えられたとき,集合Bが集合Aの一部としてすっぽり入っているとき,集合Bは集合Aの部分集合(subset) であるという. もう少し堅い定義をすると,集合Bの任意の要素(あらゆる要素)が集合Aに属するとき,集合Bは集合Aの部分集合である,とする. 集合Bが集合Aの部分集合であることを,\(B \subset{A}\)と記す.
例えば,以下の図では集合\(A=\{5, 10, 15, 20, 25, 30, 35\}\)と集合\(B=\{10, 20, 30\}\)であり, 集合Bの要素はすべて集合Aの要素なので,\(B \subset{A}\)となる(★Quiz4★).
直積#
2つの集合AとBが与えられたとき,Aの要素とBの要素を1つずつ取り出して作れるすべての組(ペア)を集めた集合を直積集合(Cartesian productあるいはdirect product) あるいは単に直積と呼ぶ. 集合AおよびBの直積集合は\(A \times B\)と記す. 直積集合\(A \times B\)の内包的な定義は以下の通り:
\(A \times B = \{ (a, b) \ | \ a \in A, b \in B \}\).
例を見てみよう. 例えば,\(A=\{1, 3, 5\}\),\(B=\{2, 4, 6\}\)のとき,AとBの直積は
\(A \times B = \{ (1, 2), (1, 4), (1, 6), (3, 2), (3, 4), (3, 6), (5, 2), (5, 4), (5, 6) \}\)
となる.
もう1つ例を見てみよう. 直積\(\mathbb{R} \times \mathbb{R}\)は2つの実数の組の集合になる. 1つ目の\(\mathbb{R}\)の要素をx座標の値,2つ目の\(\mathbb{R}\)の要素をy座標の値とすれば,\(\mathbb{R} \times \mathbb{R}\)は2次元平面と見なすことができる.
最後に数値ではない直積の例を見てみよう. 集合\(C = \{データベース, 機械学習\}\),集合\(D=\{優, 良, 可, 不可\}\)が与えられたとき, 集合Cと集合Dの直積は,
\(C \times D = \{(データベース, 優), (データベース, 良), (データベース, 可), (データベース, 不可),\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (機械学習, 優), (機械学習, 良), (機械学習, 可), (機械学習, 不可)\}\)
となる.
関係データベースは直積と関連が深い. 高校数学では学ばなかった(と思われる)直積であるが,きっちり概念を押さえておこう(★Quiz5★).
写像#
写像とは,2つの集合間の対応づけを表すものである. 集合\(X\)に属するどの要素も,ルール\(f\)で集合\(Y\)に属するいずれかの要素に対応づけすることが可能なとき,\(f\)を「\(X\)から\(Y\)への写像」と呼ぶ. \(f\)が\(X\)から\(Y\)への写像であることを,以下のように記す.
\(f: X \to Y\)
また,写像\(f\)によって集合\(X\)の要素\(x\)が集合\(Y\)の要素\(y\)に対応することを,以下のように記す(矢印の種類が異なることに注意).
\(f: x \mapsto y\)
このとき,\(y\)を写像\(f\)による要素\(x\)の像(あるいは値) と呼び,\(f(x)\)と記すこともできる.
最も馴染みのある写像の一つは関数である. 例えば,小売店で商品を購入する際には,商品価格\(x\)に対して消費税10%分を加算した料金を支払う. 最終的な支払い料金\(y\)を計算する関数\(f\)は
\(y= f(x)= 1.1x\)
と書ける. 商品価格や最終的な支払い料金は実数であり,関数\(f\)は実数から実数への写像になるため,
\(f: \mathbb{R} \to \mathbb{R}\)
と書くことができる. また,
\(f: x \mapsto 1.1x \)
と書くこともできる.
関数ではない現実的な写像の例を示そう. 大学では,学生が履修した科目に対して「優」「良」「可」「不可」の4段階の成績が付けられることが多い. 今,集合\(S\)は学生の集合,集合\(C\)は科目の集合としたとき,集合\(S\)と\(C\)の直積集合\(S \times C\)は(考えられうる)学生の科目の履修状況と見なせる(見なすことにしよう). 例えば,\(S= \{山畑滝子, 川澄桜, ... \}\),\(C=\{線形代数, データベース, ...\}\)とすると,
\(S \times C = \{(山畑滝子, 線形代数), (山畑滝子, データベース), (川澄桜, 線形代数), ... \}\)
といった感じになる.
さて,成績の種別を表す集合を\(U = \{優, 良, 可, 不可\}\)とすると,各学生の各科目に成績を付けるという行為(\(f_{採点}\))はまさに集合\(S \times C\)から\(U\)への写像と見なすことができる. よって,以下のように書くことができる.
\(f_{採点}: S \times C \to U\)
定義域と値域#
上で写像\(f: X \to Y\)の概念を導入したが,写像元と写像先に名前を付けておくと便利なため,3つの概念を導入する.
1つ目は定義域である. 集合\(X\)から集合\(Y\)への写像\(f\)が与えられたとき,集合\(X\)を写像\(f\)の定義域と呼ぶ.
2つ目は終域である. 集合\(X\)から集合\(Y\)への写像\(f\)が与えられたとき,集合\(Y\)を写像\(f\)の終域と呼ぶ.
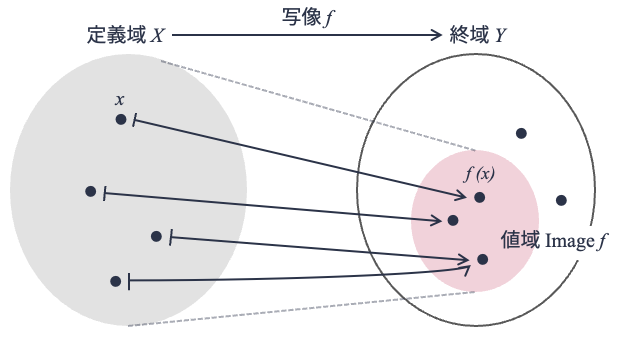
3つ目は値域である. 集合\(X\)から集合\(Y\)への写像\(f\)が与えられたとき,\(f\)によって写された集合\(X\)の要素の集合を写像\(f\)の値域と呼ぶ. 値域は\(\mathrm{Image} f\)と記される. 値域は少しややこしいが,定式化すると以下のように書ける
\(\mathrm{Image} f = \{f(x) \ | \ x \in X \}\)
終域と値域の違いが分かりづらいかもしれないが, 値域は終域の要素(\(y \in Y\))の中でも,\(y=f(x)\)を満たすような\(x\)が存在する\(y\)の集合を表す. 図にすると以下のようになる(図は「群論への第一歩(結城浩著, SBクリエイティブ)」から山本が書き起こし編集)(★Quiz6★).
クイズ#
Q1. 外延的定義#
以下の集合\(S_1\),\(S_2\),\(S_3\)を外延的定義で記せ. ただし
\(S_{name} = \{yamabata, kawasumi, tanabe\}\)
関数\(f(x)\)は文字列xを”x@nagoya-c.ac.jp”という文字列に変換する関数
とする.
\(S_1 = \{2x \ | \ x \in \mathbb{N}, 1 \leq x \leq 10 \}\)
\(S_2 = \{3x \ | \ x \in \mathbb{N}, x < 6 \}\)
\(S_3 = \{f(x) \ | \ x \in S_{name}\}\)
Q2. 内包的定義#
以下の集合\(S_4\),\(S_5\),\(S_6\)を内包的定義で記せ.
\(S_4 = \{-3, -2, -1, 0, 1, 2, 3\}\)
\(S_5 = \{3, 8, 13, 18, 23 \}\)
\(S_6 = \{-3, -8, -13, -18, -23 \}\)
Q3. 和集合,積集合,差集合#
上記Q1およびQ2で扱った集合をもとに,以下の集合の要素を求めよ.
\(S_7 = S_1 \cup S_2\)
\(S_8 = S_1 \cap S_2\)
\(S_9 = S_1 - S_2\)
\(S_{10} = S_2 - S_1\)
Q4. 部分集合#
集合\(A\),\(B\),\(C\)を以下のように定義する.
\(A = \{線形代数, 微分積分\}\)
\(B = \{線形代数, 微分積分, データ構造, データベース, 機械学習\}\)
\(C = \{\{線形代数, 微分積分\}, B \}\)
このとき,以下の1からの命題が真か偽かを求めよ.
\(データベース \in B\)
\(データベース \subset B\)
\(A \in B\)
\(A \subset B\)
\(A \in C\)
\(A \subset C\)
\(|A| = |B|\)
\(|A| = |C|\)
※ 本問題は書籍「群論への第一歩: 集合、写像から準同型定理まで」に掲載された問題の改題である.
Q5. 直積#
集合\(S_{pref}\)および\(S_{city}\)を以下のように定義する.
\(S_{pref} = \{愛知, 岐阜, 三重\}\)
\(S_{city} = \{名古屋, 岐阜, 津, 京都\}\)
このとき,集合\(S_{pref} \times S_{city}\) の要素をすべて求めよ.
Q6. 写像#
Q5で扱った集合\(S_{pref}\)と\(S_{city}\)を再び用いる.
写像\(f\)は集合\(S_{pref} \times S_{city}\)から集合\(\mathbb{R}\)の写像であり, \(p \in S_{pref}\),\(c \in S_{city}\)に対して,
と定義する.
写像\(f\)の定義域,値域,像を列挙せよ.
\(S = \{(x, y) | \ (x, y) \in S_{pref} \times S_{city}, f(x, y) = 1\}\)となる集合\(S\)の要素を求めよ.